Stability has always been the Holy Grail in quantum computing, yet as elusive as a shadow. Now, imagine an intricate, never-ending pattern, like an infinite maze with no repeating paths. This is the world of Penrose tilings, a fascinating mathematical concept that has recently found an unexpected ally in quantum computing, according to a paper on arxiv.org.

Penrose tilings, discovered by Roger Penrose in the 1970s, defy the norm of periodic repetition. These aperiodic patterns create an infinite tapestry of unique configurations, akin to a puzzle that never looks the same twice. Interestingly, it’s this uniqueness that bridges the gap between a mathematical curiosity and a groundbreaking application in quantum error correction.
The key to this alliance lies in a shared principle: local indistinguishability. Quantum computing thrives on qubits existing in superpositions, but this state is as fragile as it is powerful. The slightest disturbance, a mere nudge from an external interaction, can collapse these superpositions, derailing computations. Traditional quantum error-correcting codes attempt to shield this delicate state by distributing quantum information across a network of qubits, somewhat akin to a group of spies, each holding a fragment of a larger secret. But even this clever distribution isn’t immune to errors.
Enter Penrose tilings. Their aperiodic nature ensures that no single area holds enough information to reveal the pattern of the whole. Translating this property into the quantum realm, it suggests a quantum error-correcting code where information is so diffusely encoded that local errors have minimal impact. This approach can potentially enhance the resilience of quantum computations significantly, as it tackles the core challenge of quantum fragility head-on.
However, while the theory is sound and strikingly elegant, practical implementation remains a steep mountain to climb. The complexity of Penrose tilings and the continuous, non-discrete nature of their patterns pose significant challenges in adapting them to the discrete and finite world of quantum computing as we know it.
Decoding Quantum Error Correction
At its core, Quantum Error Correction is a method designed to protect quantum information from decoherence and other quantum noise. Unlike classical error correction, which relies on redundancy and can simply replicate bits for safety, quantum error correction faces a unique challenge: the no-cloning theorem. This theorem prevents the direct copying of quantum information, necessitating a more sophisticated approach to preserving the integrity of quantum data.
The brilliance of quantum error correction lies in its ability to distribute the information of one qubit onto a highly entangled state of several qubits. Imagine a network where each qubit is connected in a complex web of relationships, where the information of one qubit is dispersed across this network. By doing so, QEC shields quantum information from errors that could arise from faulty quantum gates, preparation, or measurements, thus enabling algorithms of greater complexity and depth.
One of the first methods of quantum error correction was discovered by Peter Shor, who found a way to store the information of one qubit onto a highly entangled state of nine qubits. The Shor code, as it came to be known, was a pioneering step in the field of quantum error correction, demonstrating that it was indeed possible to protect quantum information against decay and error.
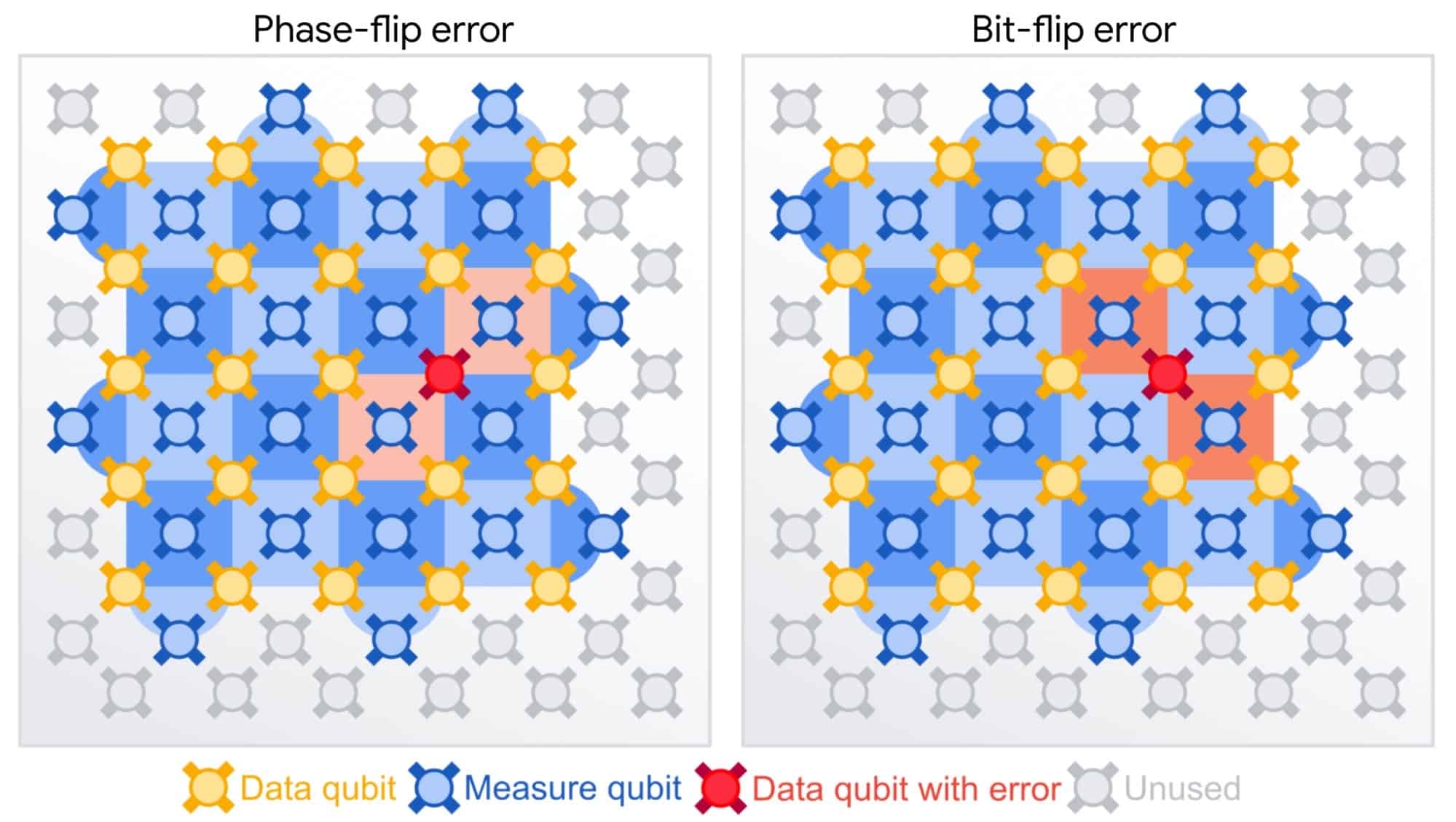
The principle behind quantum error correction involves the use of syndrome measurements. These measurements diagnose the type of error that has corrupted an encoded state and provide a means to reverse this error without disturbing the quantum information in the encoded state. This is crucial because any direct measurement of quantum information can collapse its probabilistic nature, thereby destroying the information itself. By employing syndrome measurements, QEC circumvents this problem, providing a way to correct errors without risking the integrity of the quantum information.
Apart from the Shor code, several other quantum error correction codes and techniques have been developed. These include the bit flip code, the sign flip (or phase flip) code, and various bosonic codes, among others. Each of these codes has its unique mechanism and is suited to correct specific types of errors.
One of the most intriguing aspects of quantum error correction is its applicability to various physical systems. From nuclear magnetic resonance qubits to trapped ions and superconducting qubits, the principles of QEC have been adapted and tested in multiple experimental setups. Recent advancements even include the development of topological quantum codes and the entanglement-assisted stabilizer formalism, further expanding the scope and potential of QEC.
The goal of achieving fault-tolerant quantum computing is central to the advancement of the field. The quantum threshold theorem asserts that it is possible to correct for all errors in a quantum computation if the error rate of individual quantum gates is below a certain threshold. This theorem underlines the importance of QEC in realizing practical, reliable quantum computing.
Quantum Error Correction is not just a theoretical concept but a practical necessity for the advancement of quantum computing. It offers a pathway to overcome the inherent fragility of quantum states, bringing us closer to harnessing the full potential of quantum technology. As research continues and new codes are developed, the dream of a stable, fault-tolerant quantum future becomes increasingly attainable.

